状压dp

题目特点描述：如果是传统dfs类的题目，数据范围一般给到6~8这个级别，而如果给到10以上，或者说350场周赛t3的14，很有可能就是状压dp的思路了。状压就是2^n那种想法，每个位置可以选或者不选这样的。

注意dfs思路的时间复杂度应该是O(n*n!)这个级别的，8*8!=322560就是一个1e5的级别了，然后11*11!=439084800就是一个1e8可能被卡常的级别了，所以这个题目的14数量级，用dfs的思路应该一开始就想到是过不去的

灵茶山艾府（0x3F文章）：https://leetcode.cn/circle/discuss/CaOJ45/

LeetCode 2741-特别的排列

题目大意

给你一个下标从 0 开始的整数数组 nums ，它包含 n 个 互不相同 的正整数。如果 nums 的一个排列满足以下条件，我们称它是一个特别的排列：

• 对于 0 <= i < n - 1 的下标 i ，要么 nums[i] % nums[i+1] == 0 ，要么 nums[i+1] % nums[i] == 0 。

请你返回特别排列的总数目，由于答案可能很大，请将它对 10^9 + 7 取余 后返回。

示例1：

输入：nums = [2,3,6]
输出：2
解释：[3,6,2] 和 [2,6,3] 是 nums 两个特别的排列。

示例2：

输入：nums = [1,4,3]
输出：2
解释：[3,1,4] 和 [4,1,3] 是 nums 两个特别的排列。

提示：

• 2 <= nums.length <= 14
• 1 <= nums[i] <= 10^9

分析和解答（from 灵茶山艾府）

https://www.bilibili.com/video/BV1Hj411D7Tr/?spm_id_from=333.337.search-card.all.click&vd_source=2654875159ed89b917fffce42a65196d

LeetCode经典题目是全排列，那个题目的数据范围只有6，全排列的时间复杂度是O(n!)差不多，10!差不多是10^6次方，14!明显超了

剪枝？实际上有一种情况根本无法剪枝，就是无论怎么排，都能满足他这个条件，也就是肯定能构造出一组这样的case，就没法剪枝了

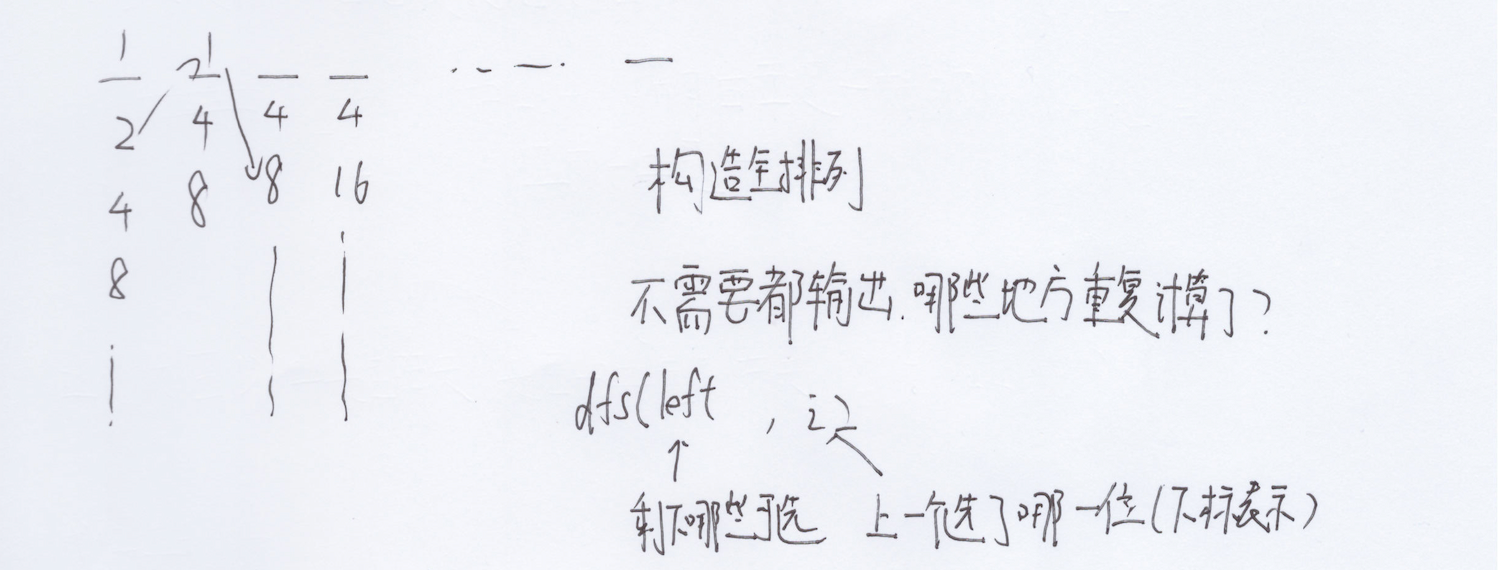
构造：1,2,4,8,16,32,64 …，无论怎么选肯定是：要么 nums[i] % nums[i+1] == 0 ，要么 nums[i+1] % nums[i] == 0 ，回溯必超，借着回溯的思路继续讲，是否有重复的计算？如果有重复的计算就可以用记忆化搜索！！

注意：记忆化搜索只能记忆dfs(i, j)这样的，不能记忆化list这种类型的作为参数！

class Solution:
    def specialPerm(self, nums: List[int]) -> int:
        # 1. 排列型回溯
        # 2. 记忆化搜索 / 递推
        # 3. 集合翻译成二进制/位运算

        # 时间复杂度  = O(状态个数) * O(单个状态的计算时间)
        #           = i是2^n，j是n，状态个数是(n*2^n)；；单个状态计算时间，for循环(n)
        #           = O(n^2 * 2^n)
        MOD =  10 ** 9 + 7
        @cache
        def dfs(i: int, j: int) -> int:  # i是集合，j是上一个选的位置，返回个数
            if i == 0:
                return 1
            res = 0
            for k, x in enumerate(nums):  # 枚举位置和数字
                if (i >> k) & 1 and (nums[j]%x==0 or x%nums[j]==0):  # k在集合i里面，并且判断题目条件
                    res += dfs(i^(1<<k), k)  # 要把k从i里面去掉
            return res
        
        # 最后求一个sum
        n = len(nums)
        u = (1 << n) - 1
        return sum(dfs(u ^ (1<<i), i) for i in range(n)) % MOD