数位dp：记忆化搜索中可以带着数字和bool！

1. 题目特点描述 + 例题：LeetCode 2376. 统计特殊整数

题目特点描述：这种题目是非常非常经典能一眼看出来的，统计1~n或者num1~num2区间内，所有满足某种条件整数的个数。而且题目数值范围给的区间会非常大，可能会到10^9这种级别的数据量

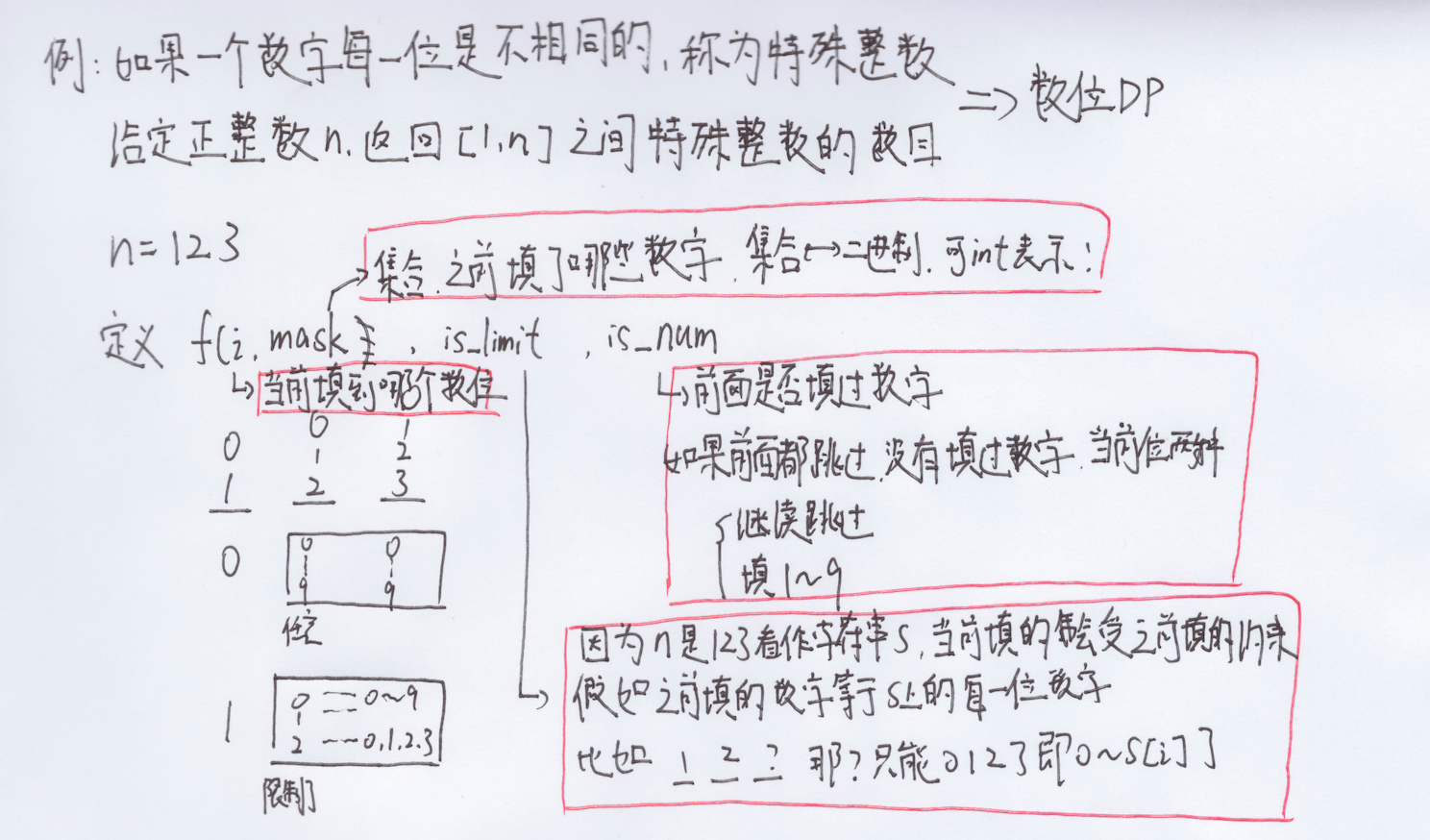
经典题目描述示例：如果一个正整数每一个数位都是互不相同的，我们称它是特殊整数。给一个正整数n，返回区间[1,n]之间特殊整数的数目。例如1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20，这其中只有11不是特殊整数，所以返回19

# 数位dp模板如下，以这个题目为例，这里是记忆化搜索的话写成python3的形式了
class Solution:
    def countSpecialNumbers(self, n: int) -> int:
        # 数位dp
        s = str(n)  # 把n转成字符串的形式
        
        # 返回从i开始填数字，i前面填的数字的集合是mask，此时能够造出的特殊整数的数目
        # is_limit 表示前面填的数字是否**都是**n对应位上的，如果为True那么当前位至多为int(s[i])，否则至多为9
        # is_num 表示前面是否填了数字（是否跳过），如果为True那么当前位可以从0开始，如果为False那么我们可以直接跳过或者从1开始填数字
        @cache
        def f(i: int, mask: int, is_limit: bool, is_num: bool) -> int:
            # 判断终点，到达终点后如果之前填过数字那么返回1表示已经构造出一个特殊整数了，否则return0
            if i == len(s):
                return int(is_num)
            res = 0
            if not is_num:  # 如果不是数字的话，选择跳过不填数字
                res = f(i+1, mask, False, False)
            # 上界，如果is_limit则是s[i]这个位置的值，否则是9
            up = int(s[i]) if is_limit else 9
			# 枚举数字
            for d in range(0 if is_num else 1, up+1):  # 这里决定了如果给1234，那么不会走到1235的情况
                # 判断一下mask里面有没有d，首先这里mask虽然是一个int但是代表了一个数组！
                # mask很巧妙的0-9这种的，第几位就代表有没有
                if mask >> d & 1 == 0:  
                    res += f(i+1, mask|(1<<d), is_limit and d == up, True)  # 如果满足条件我要选的话，就把1左移d位那个地方放上
            return res
       
        return f(0, 0, True, False)

2. 灵活变通，LeetCode 902. 最大为N的数字组合

2.1 题目大意&思路

https://leetcode.cn/problems/numbers-at-most-n-given-digit-set/

给定一个按非递减顺序排列的数字数组 digits 。你可以用任意次数 digits[i] 来写的数字。例如，如果 digits = ['1','3','5']，我们可以写数字，如 '13', '551', 和 '1351315'。

返回可以生成的小于或等于给定整数 n 的正整数的个数

思路：按照上面的模板套一下，因为不需要每个数字都不一样了，所以不需要mask了。在下面for循环取数的时候，直接for in digits这里面的数字，然后超过up就break掉。这个地方注意题目给的是字符串，需要根据字符串来魔改一下

class Solution:
    def atMostNGivenDigitSet(self, digits: List[str], n: int) -> int:
        # 数位dp
        s = str(n)  # 把n转成字符串的形式
        
        # 返回从i开始填数字，i前面填的数字的集合是mask，此时能够造出的特殊整数的数目
        # is_limit 表示前面填的数字是否**都是**n对应位上的，如果为True那么当前位至多为int(s[i])，否则至多为9
        # is_num 表示前面是否填了数字（是否跳过），如果为True那么当前位可以从0开始，如果为False那么我们可以直接跳过或者从1开始填数字
        @cache
        def f(i: int, mask: int, is_limit: bool, is_num: bool) -> int:
            # 判断终点，到达终点后如果之前填过数字那么返回1表示已经构造出一个特殊整数了，否则return0
            if i == len(s):
                return int(is_num)
            res = 0
            if not is_num:  # 如果不是数字的话，选择跳过不填数字
                res = f(i+1, None, False, False)
            # 上界
            up = int(s[i]) if is_limit else 9
			# 枚举要填的数字，枚举的范围取决于is_limit和is_num
            for d in range(0 if is_num else 1, up+1):  # 这里决定了如果给1234，那么不会走到1235的情况
                if str(d) in digits:
                    res += f(i+1, None, is_limit and d == up, True)  # 如果满足条件我要选的话，就把1左移d位那个地方放上
                else:
                    continue
            return res
       
        # 这个题实际用不到mask了，is_limit还是用得到的
        return f(0, None, True, False)

3. LeetCode 2719. 统计整数数目

3.1 题目大意

https://leetcode.cn/problems/count-of-integers/

给你两个数字字符串 num1 和 num2 ，以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件，我们称它是一个好整数：

num1 <= x <= num2
min_sum <= digit_sum(x) <= max_sum.

请你返回好整数的数目。答案可能很大，请返回答案对 10^9 + 7 取余后的结果。

注意，digit_sum(x) 表示 x各位数字之和。

示例1：

1
2
3

输入：num1 = "1", num2 = "12", min_num = 1, max_num = 8
输出：11
解释：总共有 11 个整数的数位和在 1 到 8 之间，分别是 1,2,3,4,5,6,7,8,10,11 和 12 。所以我们返回 11 。

示例2：

1
2
3

输入：num1 = "1", num2 = "5", min_num = 1, max_num = 5
输出：5
解释：数位和在 1 到 5 之间的 5 个整数分别为 1,2,3,4 和 5 。所以我们返回 5 。

提示：

1 <= num1 <= num2 <= 10^22
1 <= min_sum <= max_sum <= 400

3.2 分析和解答

先简单转化一下，f(num2)-f(num1)，这个在数位dp里面是很简单的思路了

在本身的基础上需要把sum这个作为一个dfs的参数，这里扩展一下变成dfs(i, mask, is_limit, is_num, sum)，其中mask（填了哪些数字），is_num（前面是否填过数字了，有些情况比如012 和120这个0就要重复判断这样的），mask和is_num这两个参数就不需要

然后这个题在dfs基础上要把sum作为一个参数，这个值来在递归终点i==len(nums)的时候控制是否符合条件

还有一个操作就是这个题给的num1不一定是符合条件的，反正就是注意把边界也判断一下，这种题目确实比较ACM如果搞不对就不好debug了

class Solution:
    def count(self, num1: str, num2: str, min_sum: int, max_sum: int) -> int:
        MOD = 10 ** 9 + 7
        def f(s: string) -> int:
            @cache  # 记忆化搜索
            def f(i: int, sum: int, is_limit: bool) -> int:
                if sum > max_sum:  # 非法
                    return 0
                if i == len(s):
                    return int(sum >= min_sum)
                res = 0
                up = int(s[i]) if is_limit else 9
                for d in range(up + 1):  # 枚举要填入的数字 d
                    res += f(i + 1, sum + d, is_limit and d == up)
                return res % MOD
            return f(0, 0, True)
        ans = f(num2) - f(num1) + (min_sum <= sum(map(int, num1)) <= max_sum)
        return ans % MOD

4. 简单同步一下0x3F题单，几个题简单解释一下

4.1 LeetCode 233. 数字1的个数

https://leetcode.cn/problems/number-of-digit-one/

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例1：

1 2	`输入：n = 13 输出：6`

示例2：

1 2	`输入：n = 0 输出：0`

提示

0 <= n <= 10^9

分析和解答：这里就是把一个数字中1出现的次数作为累加值，起到类似sum的作用

class Solution:
    def countDigitOne(self, n: int) -> int:
        # 数位dp
        s = str(n)  # 把n转成字符串的形式
        
        # 返回从i开始填数字，i前面填的数字的集合是mask，此时能够造出的特殊整数的数目
        # is_limit 表示前面填的数字是否**都是**n对应位上的，如果为True那么当前位至多为int(s[i])，否则至多为9
        # is_num 表示前面是否填了数字（是否跳过），如果为True那么当前位可以从0开始，如果为False那么我们可以直接跳过或者从1开始填数字
        @cache
        def f(i: int, mask: int, is_limit: bool, is_num: bool, cnt1: int) -> int:
            # 判断终点，到达终点后如果之前填过数字那么返回1表示已经构造出一个特殊整数了，否则return0
            if i == len(s):
                return cnt1
            res = 0
            if not is_num:  # 如果不是数字的话，选择跳过不填数字
                res = f(i+1, None, False, False, cnt1)
            # 上界，如果is_limit则是s[i]这个位置的值，否则是9
            up = int(s[i]) if is_limit else 9
			# 枚举要填的数字，枚举的范围取决于is_limit和is_num
            for d in range(0 if is_num else 1, up+1):  # 这里决定了如果给1234，那么不会走到1235的情况
                if d == 1:
                    res += f(i+1, None, is_limit and d == up, True, cnt1+1)
                else:
                    res += f(i+1, None, is_limit and d == up, True, cnt1)

            return res
       
        return f(0, None, True, False, 0)  # 为什么is_limit要初始化成True因为后面填的要受到约束；

4.2 LeetCode 面试题 17.06. 2出现的次数

https://leetcode.cn/problems/number-of-2s-in-range-lcci/

编写一个方法，计算从 0 到 n (含 n) 中数字 2 出现的次数。

示例：

1
2
3

输入: 25
输出: 9
解释: (2, 12, 20, 21, 22, 23, 24, 25)(注意 22 应该算作两次)

提示：

n <= 10^9

4.3 LeetCode 600. 不含连续1的非负整数

https://leetcode.cn/problems/non-negative-integers-without-consecutive-ones/

给定一个正整数 n ，请你统计在 [0, n] 范围的非负整数中，有多少个整数的二进制表示中不存在 连续的 1 。

示例1：

输入: n = 5
输出: 5
解释: 
下面列出范围在 [0, 5] 的非负整数与其对应的二进制表示：
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中，只有整数 3 违反规则（有两个连续的 1 ），其他 5 个满足规则。

示例2：

1 2	`输入: n = 1 输出: 2`

示例3：

1 2	`输入: n = 2 输出: 3`

提示：

1 <= n <= 10^9

分析和解答

class Solution:
    def findIntegers(self, n: int) -> int:
        s = str(bin(n))[2:]
        @cache
        def f(i: int, pre1: bool, is_limit: bool) -> int:
            if i == len(s):
                return 1
            up = int(s[i]) if is_limit else 1
            res = f(i + 1, False, is_limit and up == 0)  # 填 0
            if not pre1 and up == 1:  # 可以填 1
                res += f(i + 1, True, is_limit)  # 填 1
            return res
        return f(0, False, True)

algorithms > algotemplates

#algo-templates

数位dp

http://example.com/2023/06/20/algorithms/algo-templates/数位dp/

作者

Curious;

发布于

2023年6月20日

许可协议

状压dp 上一篇

349场LeetCode周赛下一篇