周赛综述&总结：

打完羽毛球的一场周赛哈哈哈，好累感觉思想敏捷度也跟着有点疲惫了hh，不过这也不是自己做不出来的理由！第三题自己把 22222 这种case的可能情况给推错了，也怪不了什么了hhhh，最后一题实际上就是个简单dfs，python有 @lru_cache(1000*1000) 可以偷鸡，总结来说还是第三题占用时间太长了，自己把规律推错了找错了，gg

第一题：第一题要慢慢读题，一次读明白然后就开始写，这次虽然2分半左右做完了，但是居然错了一次，好久好久没有第一次错过了。。。确实应该注意下边界条件和角标的，不能只追求快；

第二题：双重dfs（树的前序遍历）套在一起，非常暴力的做法了，这个题手速有点跟不上来了，主要还是树里的dfs没做的那么熟悉，每遇到一次就练习一下吧，这个题还是很暴力的；

第三题：像是数学找规律的题目，背后隐藏的其实是dp的内容，有点像跳台阶那种做法，可惜自己规律找错了没有写出来，具体内容写在详解里的照片中了；

第四题：存在，还有路径类的可以说是dfs的题目；而最小，走迷宫类的题目就是比较经典的bfs题目；这个题是个括号场景下的dfs题目，括号场景的题做多了就发现实际上不用栈什么的做匹配，而是直接记录左括号的数目，在一个右括号过来的时候看看左括号还有没有剩余可供匹配的就可以了，还可以参考这个题目，是个栈来判断最长满足条件的！32.最长有效括号，注意这个题的优化剪枝！

第一题：6056.字符串中最大的 3 位相同数字

题目链接

题目大意

给你一个字符串 num ，表示一个大整数。如果一个整数满足下述所有条件，则认为该整数是一个 优质整数 ：

该整数是 num 的一个长度为 3 的 子字符串 。
该整数由唯一一个数字重复 3 次组成。

以字符串形式返回 最大的优质整数 。如果不存在满足要求的整数，则返回一个空字符串 "" 。

注意：

子字符串 是字符串中的一个连续字符序列。
num 或优质整数中可能存在 前导零 。

示例1：

输入：num = "6777133339"
输出："777"
解释：num 中存在两个优质整数："777" 和 "333" 。
"777" 是最大的那个，所以返回 "777" 。

示例2：

1
2
3

输入：num = "2300019"
输出："000"
解释："000" 是唯一一个优质整数。

示例3：

1
2
3

输入：num = "42352338"
输出：""
解释：不存在长度为 3 且仅由一个唯一数字组成的整数。因此，不存在优质整数。

提示：

3 <= num.length <= 1000
num 仅由数字（0 - 9）组成

分析和解答

第一题要慢慢读题，一次读明白然后就开始写，这次虽然2分半左右做完了，但是居然错了一次，好久好久没有第一次错过了。。。确实应该注意下边界条件和角标的，不能只追求快；

另外来说的话，三个数是一样的，水仙花数hh！

class Solution(object):
    def largestGoodInteger(self, num):
        """
        :type num: str
        :rtype: str
        """
        res = -1
        for i in range(len(num)-2):
            tmp = num[i:i+3]
            if tmp[0] == tmp[1] and tmp[1] == tmp[2]:
                res = max(int(tmp), res)
        
        if res == -1:
            return ""
        else:
            return (3 - len(str(res))) * "0" + str(res)

第二题：6057.统计值等于子树平均值的节点数

题目链接

题目大意

给你一棵二叉树的根节点 root ，找出并返回满足要求的节点数，要求节点的值等于其子树中值的 平均值 。

注意：

n 个元素的平均值可以由 n 个元素求和然后再除以 n ，并 向下舍入 到最近的整数。
root 的子树由 root 和它的所有后代组成。

示例 1：

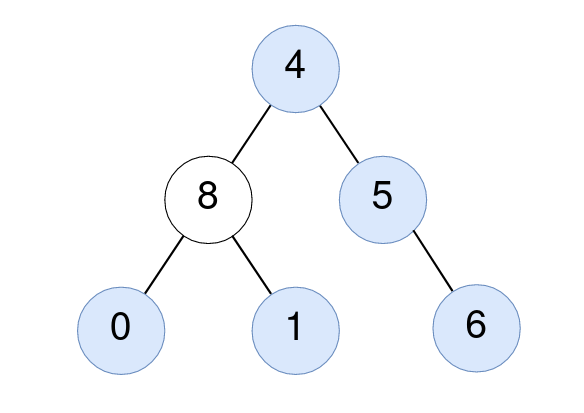
输入：root = [4,8,5,0,1,null,6]
输出：5
解释：
对值为 4 的节点：子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
对值为 5 的节点：子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
对值为 0 的节点：子树的平均值 0 / 1 = 0 。
对值为 1 的节点：子树的平均值 1 / 1 = 1 。
对值为 6 的节点：子树的平均值 6 / 1 = 6 。

示例 2：

1
2
3

输入：root = [1]
输出：1
解释：对值为 1 的节点：子树的平均值 1 / 1 = 1。

提示：

树中节点数目在范围 [1, 1000] 内
0 <= Node.val <= 1000

分析和解答

双重dfs（树的前序遍历）套在一起，非常暴力的做法了，这个题手速有点跟不上来了，主要还是树里的dfs没做的那么熟悉，每遇到一次就练习一下吧，这个题还是很暴力的；

写一个函数是 count_mean 然后再在dfs中把这个套进去！

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.cnt = 0
        self.val_sum = 0
        self.res = 0
    
    def averageOfSubtree(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        def count_mean(root):  # 统计一个子树的均值
            if root is None:
                return 0
            self.val_sum += root.val
            self.cnt += 1
            count_mean(root.left)
            count_mean(root.right)
        
        
        # 外面再套一层dfs？
        def dfs(root):
            if root is None:
                return 
            self.val_sum = 0
            self.cnt = 0
            count_mean(root)
            if self.val_sum/self.cnt == root.val:
                self.res += 1
            # print(self.cnt)
            # print(self.val_sum)
            dfs(root.left)
            dfs(root.right)
        
        dfs(root)
        return self.res

第三题：6058.统计打字方案数

题目链接

题目大意

Alice 在给 Bob 用手机打字。数字到字母的对应如下图所示。

为了打出一个字母，Alice 需要按对应字母 i 次，i 是该字母在这个按键上所处的位置。

比方说，为了按出字母 's' ，Alice 需要按 '7' 四次。类似的， Alice 需要按 '5' 两次得到字母 'k' 。
注意，数字 '0' 和 '1' 不映射到任何字母，所以 Alice 不使用它们。

但是，由于传输的错误，Bob 没有收到 Alice 打字的字母信息，反而收到了 按键的字符串信息 。

比方说，Alice 发出的信息为 "bob" ，Bob 将收到字符串 "2266622" 。

给你一个字符串 pressedKeys ，表示 Bob 收到的字符串，请你返回 Alice 总共可能发出多少种文字信息 。

由于答案可能很大，将它对 10^9 + 7 取余后返回。

示例1：

输入：pressedKeys = "22233"
输出：8
解释：
Alice 可能发出的文字信息包括：
"aaadd", "abdd", "badd", "cdd", "aaae", "abe", "bae" 和 "ce" 。
由于总共有 8 种可能的信息，所以我们返回 8 。

示例2：

输入：pressedKeys = "222222222222222222222222222222222222"
输出：82876089
解释：
总共有 2082876103 种 Alice 可能发出的文字信息。
由于我们需要将答案对 109 + 7 取余，所以我们返回 2082876103 % (109 + 7) = 82876089 。

提示：

1 <= pressedKeys.length <= 10^5
pressedKeys 只包含数字 '2' 到 '9' 。

分析和解答

像是数学找规律的题目，背后隐藏的其实是dp的内容，有点像跳台阶那种做法，可惜自己规律找错了没有写出来，具体内容写在详解里的照片中了；

另外在代码实现上，发现直接初始化所有的这种类似于离线的操作可能会超时，所以来说的话还是写了一版动态的思路，参照之前的经验，

class Solution(object):
    def countTexts(self, pressedKeys):
        """
        :type pressedKeys: str
        :rtype: int
        """

        """ 
        # 写法1，方法应该没问题，但是初始化的时候太耗时了，可能就被边界卡了
        if len(pressedKeys) == 0:
            return 0
        
        max_len = len(pressedKeys) + 5
        MOD = 10**9 + 7

        # 这个过程有点太耗时了，这里可能要换一种动态的写法，因为太多位置是没用的了？
        # 非7，9的递推方程
        f_1 = [0] * max_len  # 写不写成for好像没区别
        f_1[1], f_1[2], f_1[3] = 1, 2, 4
        # 7，9的递推方程
        f_2 = [0] * max_len
        f_2[1], f_2[2], f_2[3], f_2[4] = 1, 2, 4, 8
        # 简化为一个循环
        for i in range(4, max_len):
            f_1[i] = f_1[i-1] + f_1[i-2] + f_1[i-3]
            if i != 4:
                f_2[i] = f_2[i-1] + f_2[i-2] + f_2[i-3] + f_2[i-4]
        
        # 开始分组统计
        res = 1
        pressedKeys += '#'  # 哨兵
        now_str = pressedKeys[0]
        cnt = 1
        i = 1
        while i < len(pressedKeys):
            if pressedKeys[i] == now_str:
                cnt += 1
            else:
                if now_str == '7' or now_str == '9':
                    res *= f_2[cnt] % MOD
                else:
                    res *= f_1[cnt] % MOD
                cnt = 1
                now_str = pressedKeys[i]
            i += 1

        return res % MOD
        """

        # 写法2，把写法1的方法转成动态的，或者相对更加记忆化一点
        f_1 = [0, 1, 2, 4]  # 角标直接对应上
        f_2 = [0, 1, 2, 4, 8]
        i = 1
        cnt = 1
        pressedKeys += '#'
        now_str = pressedKeys[0]
        res = 1
        while i < len(pressedKeys):
            if pressedKeys[i] == now_str:
                cnt += 1
            else:
                if now_str == '7' or now_str == '9':
                    try:
                        res *= f_2[cnt]
                    except:
                        for j in range(len(f_2), cnt+1):
                            # 注，这里实际上不推荐append的写法，最好是初始化一个很长的，往里填
                            f_2.append(f_2[j-1] + f_2[j-2] + f_2[j-3] + f_2[j-4])
                        res *= f_2[cnt]
                else:
                    try:
                        res *= f_1[cnt]
                    except:
                        for j in range(len(f_1), cnt+1):
                            f_1.append(f_1[j-1] + f_1[j-2] + f_1[j-3])
                        res *= f_1[cnt]
                cnt = 1
                now_str = pressedKeys[i]
            i += 1

        return res % (10**9 + 7)

第四题：6059.检查是否有合法括号字符串路径

题目链接

题目大意

一个括号字符串是一个非空且只包含 '(' 和 ')' 的字符串。如果下面任意条件为真，那么这个括号字符串就是 合法的 。

字符串是 () 。
字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
字符串可以表示为 (A) ，其中 A 是合法括号序列。

给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

路径开始于左上角格子 (0, 0) 。
路径结束于右下角格子 (m - 1, n - 1) 。
路径每次只会向下或者向右移动。
路径经过的格子组成的括号字符串是合法的。

如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

示例 1：

输入：grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
输出：true
解释：上图展示了两条路径，它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 "()(())" 。
第二条路径得到的合法字符串是 "((()))" 。
注意可能有其他的合法括号字符串路径。

示例2：

1
2
3

输入：grid = [[")",")"],["(","("]]
输出：false
解释：两条可行路径分别得到 "))(" 和 ")((" 。由于它们都不是合法括号字符串，我们返回 false 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] 要么是 '(' ，要么是 ')' 。

分析和解答

存在，还有路径类的可以说是dfs的题目；而最小，走迷宫类的题目就是比较经典的bfs题目；这个题是个括号场景下的dfs题目，括号场景的题做多了就发现实际上不用栈什么的做匹配，而是直接记录左括号的数目，在一个右括号过来的时候看看左括号还有没有剩余可供匹配的就可以了，还可以参考这个题目，是个栈来判断最长满足条件的！32.最长有效括号

在优化剪枝上，一种是 @lru_cache(1000*1000) 靠着编译器来优化，另外一种是记录visited数组，类似于下面图里写的意思，还有就是说匹配上的括号长度一定是偶数的：

这个题还遇到很多玄学问题，就是说两个优化都加上就过不了，但是只留其中一个优化就可以。。。dfs结构还是比较简单的！

from functools import lru_cache

class Solution(object):
    
    def __init__(self):
        self.flag = False
        self.already_true = {}
        self.grid = None
    
    def hasValidPath(self, grid:List[List[str]]) -> bool:
        """
        :type grid: List[List[str]]
        :rtype: bool
        """
        # 只能往下，或者往右移动
        dx = [1, 0]
        dy = [0, 1]
        n = len(grid)
        m = len(grid[0])
        self.grid = grid  # n,m实际上也可以搞到self.里去

        if (n+m) % 2 == 0:
            return False


        @lru_cache(1000*1000)
        def dfs(x:int, y:int, left_kh_cnt:int, n:int, m:int) -> None:
            if left_kh_cnt < 0:
                return 

            # 剪枝条件是，路径上某个位置，在相同left_kh_cnt条件下，是否出现过了
            # 这里原理上的解释是
            if self.already_true.get((x,y,left_kh_cnt)) is None:
                self.already_true[(x,y,left_kh_cnt)] = True
                # print("self.already_true: ", self.already_true)
            else:
                return 

            if x == n-1 and y == m-1 and left_kh_cnt == 0:  # 恰好匹配
                self.flag = True
                return 
            

            # 1. 先写dfs逻辑，剩下逻辑随之适配
            for i in range(2):
                nx = x + dx[i]
                ny = y + dy[i]
                if nx >= 0 and nx < n and ny >= 0 and ny < m: 
                    if self.grid[nx][ny] == '(':
                        dfs(nx, ny, left_kh_cnt+1, n, m)
                    else:
                        dfs(nx, ny, left_kh_cnt-1, n, m)

        if self.grid[0][0] == '(' or self.grid[-1][-1] != '(':
            dfs(0, 0, 1, n, m)
        else:
            return False
        return self.flag

algorithms > leetcode-weekly-contest

#字符串 #数组 #EASY #MEDIUM #树 #深度优先搜索 #动态规划 #HARD #哈希表 #矩阵 #数学 #二叉搜索树

292场LeetCode周赛

http://example.com/2022/05/08/algorithms/leetcode-weekly-contest/292场LeetCode周赛/

作者

Curious;

发布于

2022年5月8日

许可协议

293场LeetCode周赛上一篇

正则表达式学习下一篇