124.二叉树中的最大路径和-python

124.二叉树中的最大路径和（困难）

题目大意：路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

题目

题目链接

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例1：

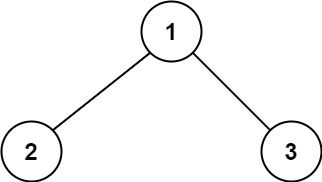
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 10^4]
• -1000 <= Node.val <= 1000

分析和解答

经典的树形子结构dp题目，这个题带了一个最大路径和，这块是要有一个全局的变量，每个子结构的值要和这个全局的值来比取最大值；

树里的子结构，一般思路就是后序遍历的思想，把每个节点当做根节点，然后求出这个点左右和这个点的值加起来，和全局的来比；而其中比较关键的是在此之前，每个地方的递归出口，也就是后序遍历的出口要把子结构的值给返回回去，而这种路径的话，子结构实际上只能往左边或者右边，也就是root.val + max(left_val, right_val)，其中两边的val需要通过递归来完成返回

总结来说，一般的套路是如下几个步骤：

1. 写 from function tools import lru_cache ，在dfs函数前加上 @lru_cache(1000*1000) 的修饰，这样可以一定程度上减小时间占用（在笔试题目中可能会有奇效hh）；
2. 写入口，入口一般有两种情况，像是笔试题目的话可能是 def dfs(left, right) 这样的，像是leetcode题目的话，可能就是 def dfs(root)；
3. 写出口返回值，一般来说就是子结构的值，如果是像这个题一样树中路径的话，就是当前节点加上左边或者右边的；
4. 写后续遍历的递归部分，将两边的子结构传入dfs函数中，来进一步往深度优先寻找；
5. 写全局比较，这个步骤不一定存在，但是如果把每个节点像这个题一样当做“中转节点”的话，那就要和全局的值比较一下；
6. 写递归出口条件，一般来说就是 root is None 或者 left >= right这类的条件；

这个模式感觉还挺套路的，几乎子结构或者带着树中路径的题目都可以这么做，也算是积累到一种做法吧，相似题目包括：

124.二叉树中的最大路径和 hard
543.二叉树直径 easy
687.最长同值路径 medium
001场笔试练习 第四题.最优二叉树

通过上边的总结来说，这个题目基本已经可以做出来了，需要注意的是这个题目中可能有负数存在，路径上带上负数还不如不带这条路径，子结构返回的时候需要注意一下

补充：

543.二叉树直径 easy: https://leetcode-cn.com/problems/diameter-of-binary-tree/

124.二叉树中的最大路径和 hard: https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/

这两个题感觉是很像的，但是不太像树形dp，就像是在树里的dfs一样，感觉最主要的思路就是子结构

• 在写dfs函数的时候，先写返回值，返回值是左右两个子结构中最大的一个加上当前节点的值；；这里说是子结构是因为他的父节点如果选了左边的就不能选右边的（题目特性决定）；；代表这个根作为子结构的条件下最大值

• 然后写结束条件，一般就是root is None的时候

• 然后写递归的两边，基本就是把root.left和root.right传进去

• 然后写全局的，全局的就是 当前+左子结构+右子结构，然后和现有比取最大的；；；代表按这个根作为真实根的情况下条件的最大值

最后return回全局的这个最大的

树里子结构的dfs

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right


class Solution(object):
    def __init__(self):
        self.max_res = -1e9
    
    def maxPathSum(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def dfs(root):
            if root is None:
                return 0

            left_max_val = dfs(root.left) # 往左子树走，以左子树为根的最大子结构
            right_max_val = dfs(root.right)  # 往右子树走，右子树的最大子结构

            tmp_value = root.val + left_max_val + right_max_val  # 以root为根的最大子结构
            self.max_res = max(self.max_res, tmp_value)
            
            # 这个return是单一子结构的return，子结构下不能同时往左又往右走，只能选择一边，子结构的！！！
            if root.val + max([0, left_max_val, right_max_val]) > 0:
                return root.val + max([0, left_max_val, right_max_val]) 
            else:
                return 0

        dfs(root)
        return self.max_res