001场笔试练习

写在第一次尝试时：笔试题目感觉和平常LeetCode题目不太一样，比较关键的是要自己构造输入并且有些场景下可能会遇到格式化输出的情况。中间的调试过程平台不同也会让人做起来不太熟练，现在感觉在刷周赛之外也要做一做笔试题，有些笔试题感觉出题思路和ACM那些比较像和周赛的考察点不太一样，这样也是为了未来做准备，并且多积累一些刷题经验吧~ 输入输出这块感觉还是挺大的坑的，整体结构上可以写成类似于LeetCode solution的形式，还有个突然想起来补充说的，笔试题感觉每次给的样例case都好简单啊，估计只能过最最简单case的那种，而且测试的时候貌似不能面向答案编程Orz；

笔试题目选择：美团2021校招笔试-编程题(通用编程试题,第10场)

笔试刷题总结：前两个题都有一种模拟的感觉，第一个题情况没考虑全但是case太弱了直接给偷过了，第二个的话就是排序简单模拟，第三个题的话一眼看过去因为有最左这种的条件在几乎一下就能看出是小根堆这个背景了，总结来看的话这次这套题前三个题甚至比周赛题还简单？第四个题是树形dp，看了看答案还是没学会，感觉像是一种树构造性的题目，感觉经验还是差太多了，还需要多做题吧，希望能在dp上更进一步，这样笔试题/面试题就都没有那么怕了，跟一波b站wls哈哈哈；补充：后来把第四题用暴力dfs的方法过了6/10，还加上了一个@lru_cache(1000*1000)；

第一题：淘汰分数

题目大意

某比赛已经进入了淘汰赛阶段,已知共有n名选手参与了此阶段比赛，他们的得分分别是a_1,a_2….a_n,小美作为比赛的裁判希望设定一个分数线m，使得所有分数大于m的选手晋级，其他人淘汰。

但是为了保护粉丝脆弱的心脏，小美希望晋级和淘汰的人数均在[x,y]之间。

显然这个m有可能是不存在的，也有可能存在多个m，如果不存在，请你输出-1，如果存在多个，请你输出符合条件的最低的分数线。

数据范围：1 ≤ n ≤ 50000，1 ≤ x ≤ y ≤ n
进阶：时间复杂度O(nlogn)，空间复杂度O(n)

输入描述：

1
2
输入第一行仅包含三个正整数n,x,y，分别表示参赛的人数和晋级淘汰人数区间。(1<=n<=50000,1<=x,y<=n)
输入第二行包含n个整数，中间用空格隔开，表示从1号选手到n号选手的成绩。(1<=|a_i|<=1000)

输出描述：

1
输出仅包含一个整数，如果不存在这样的m，则输出-1，否则输出符合条件的最小的值。

输入例子1：

1
2
6 2 3
1 2 3 4 5 6

输出例子1：

1
3

分析和解答

这个题好像出的case比较弱，做的时候直接用前后缀偷鸡了，实际上可能需要考虑同分数的情况，所以自己的前后缀做法实际上是有问题的，不过既然偷过了，就先不管了哈哈哈，就当他是笔试题和leetcode的不同了；

笔试题模板就用类似这样的，写成leetcode的写法，也会相对比较熟练了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#encoding:utf-8
class Solution(object):

    def func(self, n, x, y, scores):
        scores.sort()
        pre = 0
        last = len(scores)

        m = -1
        for i in range(len(scores)):  # 二分优化
            pre += 1
            last -= 1

            if pre >= x and pre <= y and last >= x and last <= y:
                m = scores[i]
                break

        return m


if __name__ == '__main__':
    # init solution    
    s = Solution()

    # input区域 https://blog.csdn.net/mmmmonkeyfei/article/details/118863773
    n, x, y = map(int, input().strip().split(" "))
    scores = list(map(int, input().strip().split(" ")))

    # mock区域
    # n = 6
    # x = 2
    # y = 3
    # scores = [1, 2, 3, 4, 5, 6]
    

    res = s.func(n, x, y, scores)
    print(res)

第二题：正则序列

题目大意

我们称一个长度为n的序列为正则序列，当且仅当该序列是一个由1~n组成的排列，即该序列由n个正整数组成，取值在[1,n]范围，且不存在重复的数，同时正则序列不要求排序

有一天小团得到了一个长度为n的任意序列s，他需要在有限次操作内，将这个序列变成一个正则序列，每次操作他可以任选序列中的一个数字，并将该数字加一或者减一。

请问他最少用多少次操作可以把这个序列变成正则序列？

数据范围： 1 ≤ n ≤ 20000，0 ≤ abs(s_i) ≤ 10000
进阶：时间复杂度O(n)，空间复杂度O(n) 注：这里实际上是不是写错了，时间复杂度没法做到O(n)吧

输入例子1：

1
2
5
-1 2 3 10 100

输出例子1：

1
103

分析和解答

这个题也太简单了，感觉甚至不如平常周赛第一题的包装后的难度，排个序然后对位相减就可以，O(nlogn)的解法如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#encoding:utf-8
class Solution(object):

    def func(self, n, nums):
        nums.sort()
        res = 0
        for i in range(len(nums)):
            res += abs(nums[i] - (i+1))

        return res

if __name__ == '__main__':
    # init solution    
    s = Solution()

    # input区域 https://blog.csdn.net/mmmmonkeyfei/article/details/118863773
    n = map(int, input().strip().split(" "))
    nums = list(map(int, input().strip().split(" ")))

    # mock区域
    # n = 5
    # nums = [-1, 2, 3, 10, 100]
    
    res = s.func(n, nums)
    print(res)

第三题：公司食堂

题目大意

小美和小团所在公司的食堂有N张餐桌，从左到右摆成一排，每张餐桌有2张餐椅供至多2人用餐，公司职员排队进入食堂用餐。小美发现职员用餐的一个规律并告诉小团：当男职员进入食堂时，他会优先选择已经坐有1人的餐桌用餐，只有当每张餐桌要么空着要么坐满2人时，他才会考虑空着的餐桌；

当女职员进入食堂时，她会优先选择未坐人的餐桌用餐，只有当每张餐桌都坐有至少1人时，她才会考虑已经坐有1人的餐桌；

无论男女，当有多张餐桌供职员选择时，他会选择最靠左的餐桌用餐。现在食堂内已有若干人在用餐，另外M个人正排队进入食堂，小团会根据小美告诉他的规律预测排队的每个人分别会坐哪张餐桌。

进阶：时间复杂度O(nlogn)，空间复杂度O(n)

输入描述：

1
2
3
4
5
6
7
8
9
第一行输入一个整数T（1<=T<=10），表示数据组数。

每组数据占四行，第一行输入一个整数N（1<=N<=500000）；

第二行输入一个长度为N且仅包含数字0、1、2的字符串，第i个数字表示左起第i张餐桌已坐有的用餐人数；

第三行输入一个整数M（1<=M<=2N且保证排队的每个人进入食堂时都有可供选择的餐桌）；

第四行输入一个长度为M且仅包含字母M、F的字符串，若第i个字母为M，则排在第i的人为男性，否则其为女性。

输出描述：

1
每组数据输出占M行，第i行输出一个整数j（1<=j<=N），表示排在第i的人将选择左起第j张餐桌用餐。

输入示例1：

1
2
3
4
5
1
5
01102
6
MFMMFF

输入示例2：

1
2
3
4
5
6
2
1
1
3
4
4

分析和解答

感觉是个模拟题，本来以为笔试会经常出这种模拟题的，但是从今年来看好像不是这样啊。当有多张餐桌供职员选择时，他会选择最靠左的餐桌用餐 这感觉是一个提示，提示使用优先队列做模拟；

现在来看这个题好像一下想过去也不是能秒做的题目，但是感觉那天状态比较好吧？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#encoding:utf-8
class Solution(object):

    def func(self, n, sitdown_peoples, m, gender):
        res_list = []
        have_zero_count = 0
        have_one_count = 0
        have_two_count = 0

        import heapq
        mapping = {0: [], 1: [], 2: []}  # 每个list是priority queue（heapq）

        for i in range(len(sitdown_peoples)):
            mapping[sitdown_peoples[i]].append(i)
        # heapify一下，优先队列
        for i in range(3):
            heapq.heapify(mapping[i])

        # print("after mapping: ", mapping)

        for i in range(len(gender)):
            if gender[i] == 'M':
                # 男员工会优先选择有一个人的地方坐，如果都有了就去坐两个空的
                if len(mapping[1]) != 0:  # 优先选择有一个人的地方坐
                    # 坐在这里
                    tmp_idx = heapq.heappop(mapping[1])
                    res_list.append(tmp_idx)
                    # 修改状态
                    heapq.heappush(mapping[2], tmp_idx)

                else: # 去坐两个空的
                    tmp_idx = heapq.heappop(mapping[0])
                    res_list.append(tmp_idx)
                    # 修改状态
                    heapq.heappush(mapping[1], tmp_idx)

            else:
                # 女员工会优先选择都空的地方坐，如果没有了才会和别人拼桌
                if len(mapping[0]) != 0:  # 优先选择没有人的地方
                    # 坐在这里
                    tmp_idx = heapq.heappop(mapping[0])
                    res_list.append(tmp_idx)
                    # 修改状态
                    heapq.heappush(mapping[1], tmp_idx)

                else: # 去坐有人的
                    tmp_idx = heapq.heappop(mapping[1])
                    res_list.append(tmp_idx)
                    # 修改状态
                    heapq.heappush(mapping[2], tmp_idx)

        return res_list

        


if __name__ == '__main__':
    # init solution    
    s = Solution()

    # input区域 https://blog.csdn.net/mmmmonkeyfei/article/details/118863773
    t = int(input().strip())

    for _ in range(t):
        n = int(input().strip())
        sitdown_peoples = list(map(str, input()))
        sitdown_peoples = [int(item) for item in sitdown_peoples]
        m = int(input().strip())
        gender = list(map(str, input()))


        # print("n: ", n)
        # print("sitdown_peoples: ", sitdown_peoples)
        # print("m: ", m)
        # print("gender: ", gender)

        res_list = s.func(n, sitdown_peoples, m, gender)
        # print("res_list: ", res_list)

        for i in range(len(res_list)):
            print(res_list[i]+1)

第四题：最优二叉树II

题目大意

小团有一个由N个节点组成的二叉树，每个节点有一个权值。定义二叉树每条边的开销为其两端节点权值的乘积，二叉树的总开销即每条边的开销之和。小团按照二叉树的中序遍历依次记录下每个节点的权值，即他记录下了N个数，第i个数表示位于中序遍历第i个位置的节点的权值。之后由于某种原因，小团遗忘了二叉树的具体结构。在所有可能的二叉树中，总开销最小的二叉树被称为最优二叉树。现在，小团请小美求出最优二叉树的总开销。

输入描述：

1
2
第一行输入一个整数N（1<=N<=300），表示二叉树的节点数。
第二行输入N个由空格隔开的整数，表示按中序遍历记录下的各个节点的权值，所有权值均为不超过1000的正整数。

输出描述：

1
输出一个整数，表示最优二叉树的总开销。

输入例子1：

1
2
5
7 6 5 1 3

输出例子1：

1
45

例子说明1：

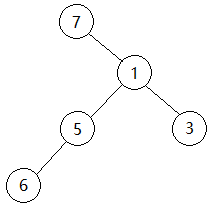
1
最优二叉树如图所示，总开销为7*1+6*5+5*1+1*3=45。

分析和解答

这个题后来看了答案，好像是要区间dp的做法，但是区间dp感觉就是完全未知的领域了，树上的操作感觉实在是太多了，包括还有线段树一类的，说到这里也什么时候找个线段树的模板，以备之后套用吧

这个题也可以用树形dp直接暴力，而且这里学到一个lru_cache，对于笔试题感觉是一种偷鸡的操作，让本来只能过2/10的测试用例瞬间变到过6/10 ~ 7/10了，感觉就是dfs中的一个笔试偷鸡操作？应该所有dfs都可以用吧！

1
2
3
4
5
from functiontools import lru_cache

@lru_cache(1000*1000)
def dfs():
    # do sth

这个题暂时只学习了下dfs暴力的方法了，和子结构树形dp很像，但是和leetcode那边的区别是这里的输入是一个数组，所以dfs的区间是 (0, n) 这种感觉，然后dfs的含义感觉就是把 i 作为子结构的根节点，然后i这个位置乘父亲的，再加上左边和右边的，就完成了一次内部的递归，此外，在内部递归中要遍历每个 i 位置，即每次（包括dfs下去的子层）都要把这个地方当做根节点试一下，最后记录一个局部子结构的ret最优作为返回值，而 (0, n) 这个子结构实际上就是父结构了，另外每次要把 parent_value 往下传下去；

子结构dp，LeetCode相似题目：

687.最长同值路径 medium
124.二叉树中的最大路径和 hard
543.二叉树直径 easy

如下代码可以通过6/10 ~ 7/10组测试用例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#encoding:utf-8
from functools import lru_cache

class Solution(object):
    def func(self, n, values):
        # 输出的values是一个global的数组，这里lru_cache大幅优化效率
        @lru_cache(1000*1000)
        def dfs(left, right, parent_val):

            # 3. 写出口，这里等于的话，就0
            if left >= right:
                return 0

            # 1. 先写返回值，这里是子结构返回值，每个子结构都初始化一个inf值
            res = 1e9

            # 2. 递归这个left,right区间下的最优子结构
            for i in range(left, right):
                left_val = dfs(left, i, values[i])
                right_val = dfs(i+1, right, values[i])
                res = min(res, values[i] * parent_val + left_val + right_val)


            # 1. 先写返回值，这里是子结构返回值，每个子结构都初始化一个inf值
            return res

        return dfs(0, n, 0)


if __name__ == '__main__':
    # init solution    
    s = Solution()

    # input区域 https://blog.csdn.net/mmmmonkeyfei/article/details/118863773
    n = int(input().strip())
    global values
    values = list(map(int, input().strip().split(" ")))

    # print("n: ", n)
    # print("values: ", values)
    

    # 调用以及output
    res = s.func(n, values)
    print(res)
LeetCode-python
#模拟 #数组 #排序 #堆 #优先队列 #EASY #MEDIUM
001场笔试练习
http://example.com/2022/04/26/algorithms/001场笔试练习/
作者
Curious;
发布于
2022年4月26日
许可协议